たわみ角・たわみの公式は暗記すると思いますが、忘れたときのために算出方法を紹介します。
基本的には曲げモーメントを1回積分するとたわみ角、2回積分するとたわみが求められます。
ここでは片持ち梁の集中荷重の場合を求めてみます。
1.曲げモーメントを求める
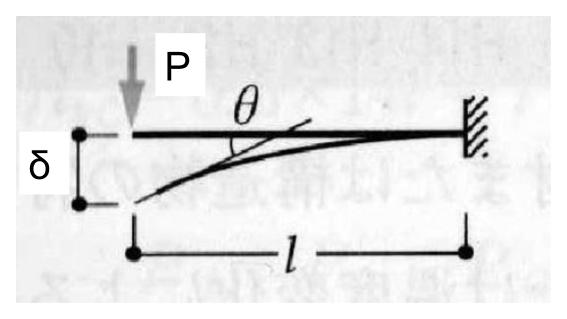
$$M=-Px$$
$$EI \frac{d^2 y}{dx^2} \ =-M=Px$$
2.たわみ角を求める
$$曲げモーメントを積分すると\hspace{4cm}$$
$$\ EI \frac{dy}{dx} \ =\int {Px} \, dx =\frac{P}{2}x^2+c_1\ $$
$$固定端部(x=l)でたわみ角 (\frac{dy}{dx} =0)なので$$
$$\frac{P}{2}l^2+c_1=0 \hspace{1cm} c_1=-\frac{P}{2}l^2$$
$$\frac{dy}{dx} =θ \hspace{1cm} c_1=-\frac{P}{2}l^2 を代入すると$$
$$\ EIθ =\frac{P}{2}x^2-\frac{P}{2}l^2 $$
$$θ =\frac{P(x^2-l^2)}{2EI}$$
$$最大たわみ角はx=0のときなので$$
$$θ =\frac{Pl^2}{2EI}$$
3.たわみを求める
$$たわみ角を積分すると\hspace{4cm}$$
$$\ EIδ\ =\int (\frac{P}{2}x^2+c_1) \, dx =\frac{P}{6}x^3+c_1x+c_2\ $$
$$固定端部(x=l)でたわみ (y=0)なので$$
$$\frac{P}{6}l^3+c_1l+c_2=0 $$
$$たわみ角を求めたときよりc_1=-\frac{P}{2}l^2 \hspace{1cm} c_2=\frac{P}{3}l^3$$
$$代入すると $$
$$EIδ=\frac{P}{6}x^3-\frac{P}{2}l^2x+\frac{P}{3}l^3$$
$$δ=\frac{P(x^3-3l^2x+2l^3)}{6EI}$$
$$最大たわみはx=0のときなので$$
$$δ=\frac{Pl^3}{3EI}$$
以上になります。たわみとたわみ角は基本暗記で良いと思いますが、
もし忘れたときのために算出方法を確認してくと良いです。
- たわみ角は1回積分なのでlの2乗、2乗なので分母も2
- たわみ は2回積分なのでlの3乗、3乗なので分母も3



